※Word文書をプレビューで表示している場合、表記にズレが生じる可能性があります。
データをダウンロードした際には正しく表記されます。
◆はじめに
小学校の図形指導において、「角度の大きさ」に対する感覚を身に付けさせることはとても重要です。中でも、三角定規を活用して様々な角度を作る活動は、子どもたちが身近な教具を通して角度の性質に気づき、思考を深める良い機会になります。
今回は、2枚の三角定規を組み合わせることでどのような角度が作れるのかについて解説し、そのまま授業で使える指導案のアイディアも紹介します。
◆三角定規の基本
まず、用いる三角定規は次の2種類です。
- 30°-60°-90° の三角定規(直角三角形)
- 45°-45°-90° の三角定規(直角二等辺三角形)

これらの定規を1枚だけ使った場合、次の角度を簡単に作ることができます。
- 30°、45°、60°、90°
◆三角定規を2枚使って作る角度
では、2枚の三角定規を組み合わせて使うと、どのような角度を作れるでしょうか。子どもたちが「角度を組み合わせる」という発想に触れながら、論理的思考を育むチャンスです。
◆作ることができる角度
| 組み合わせ | 作れる角度 | 説明 |
|---|---|---|
30° + 45° 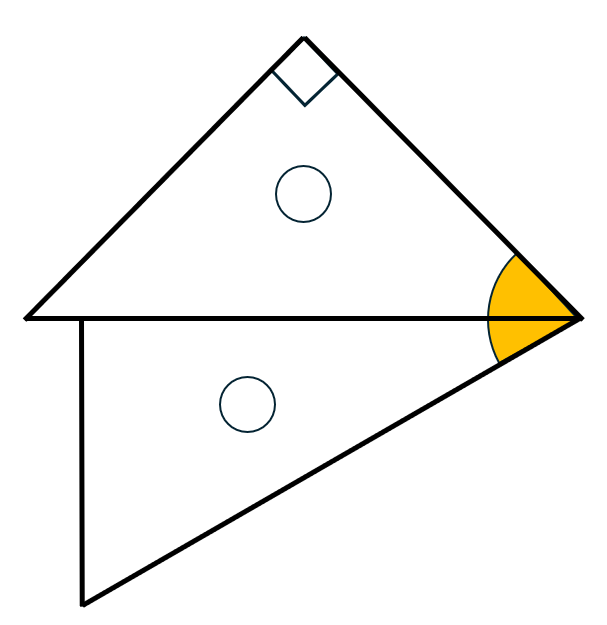 | 75° | 2つの異なる定規の角を合わせる |
45° + 60° 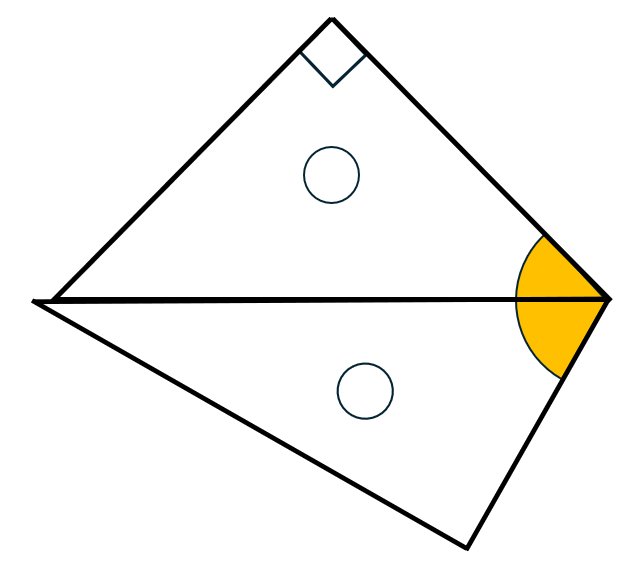 | 105° | 異なる角の和を作る |
30° + 90° 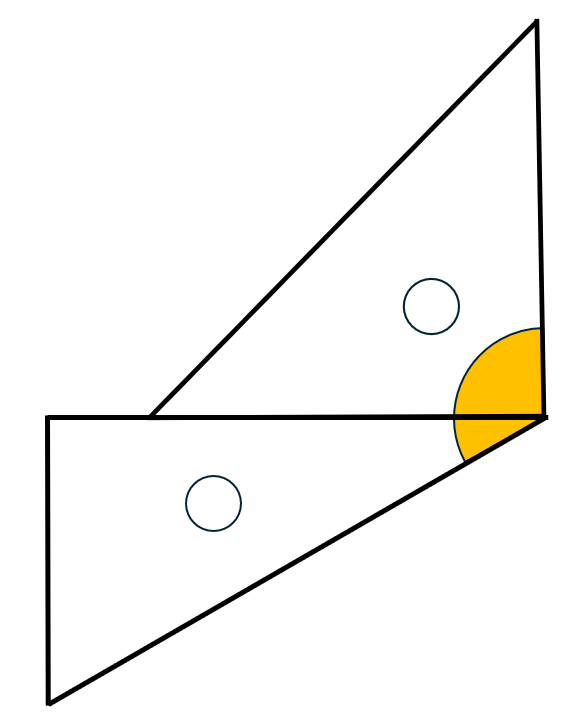 | 120° | 直角と鋭角の組み合わせ |
45° + 90° 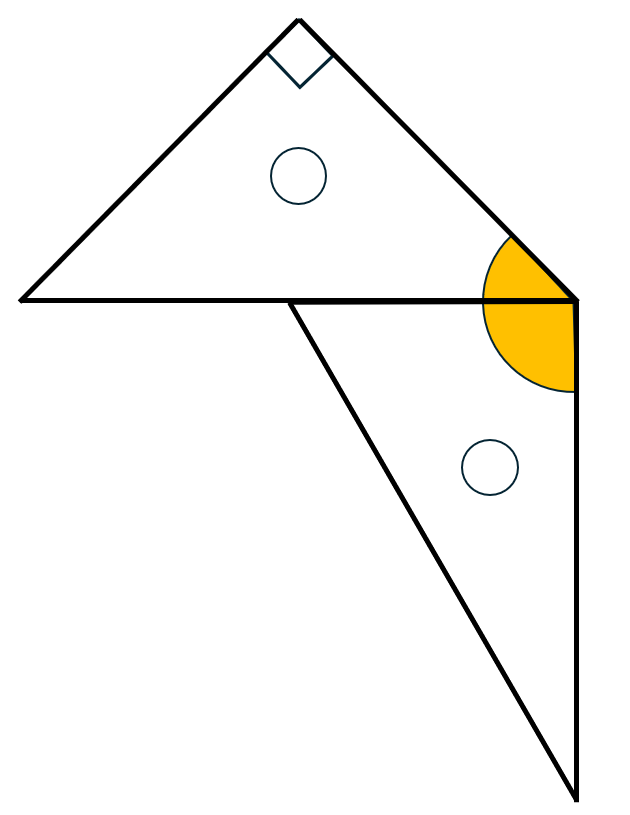 | 135° | 直角と直角二等辺三角形の角 |
60° + 90° 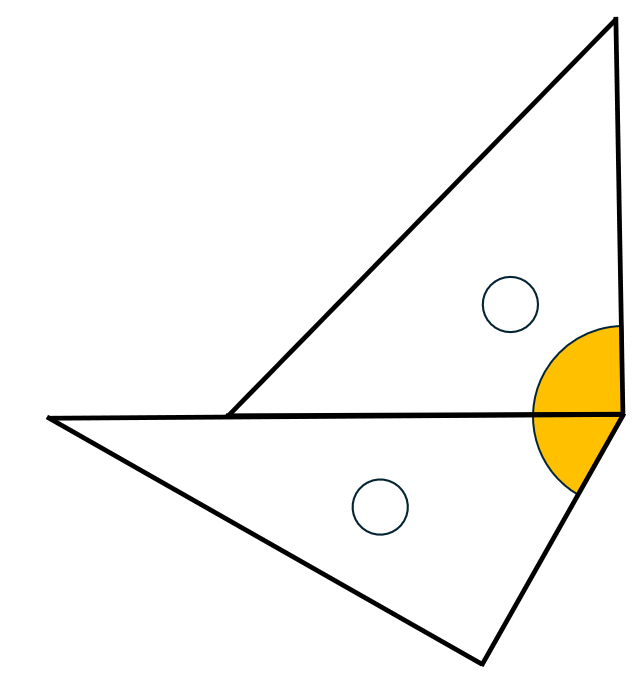 | 150° | 鋭角と直角の組み合わせ |
90° + 90° 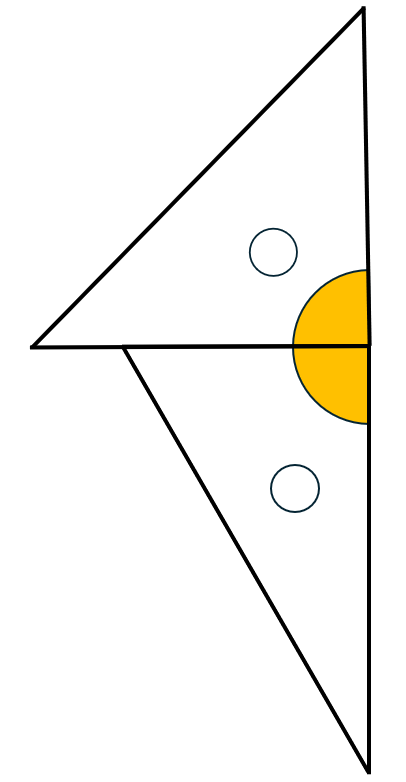 | 180° | 2枚の直角を合わせる |
45° の上に 30° を重ねる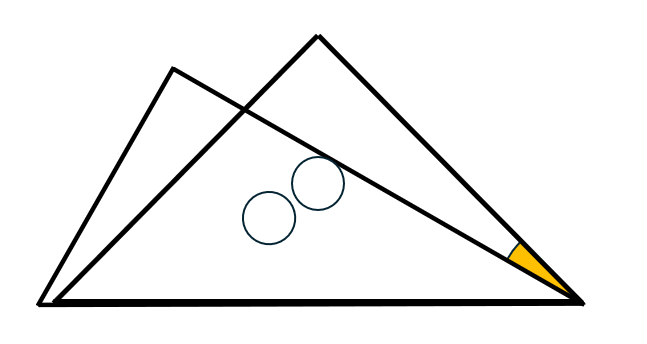 | 15° | 角度の差を使う発展的な考え方 |
※実際には、「重ねる」「合わせる」「隙間を作る」など、角の作り方は子どもの自由な発想が生きる場面です。様々な作り方があるので多様な考えを出させたいです。
◆できた角度のまとめ
これまでの活動で作れた角度を整理してみましょう。
15°、30°、45°、60°、75°、90°、105°、120°、135°、150°、180°
このように、15°刻みで作れることに気づくと、子どもたちの中から次のような問いが生まれるかもしれません。
◆発展的な問い「165°は作れないのか?」
165°だけが抜けていることに気づくでしょう。ここで、思考を発展させるための活動を取り入れましょう。
◆165°を作る工夫
- 三角定規を交差させるように置き、30°の鋭角の外側と45°の鋭角の外側で作られる角度を観察します。
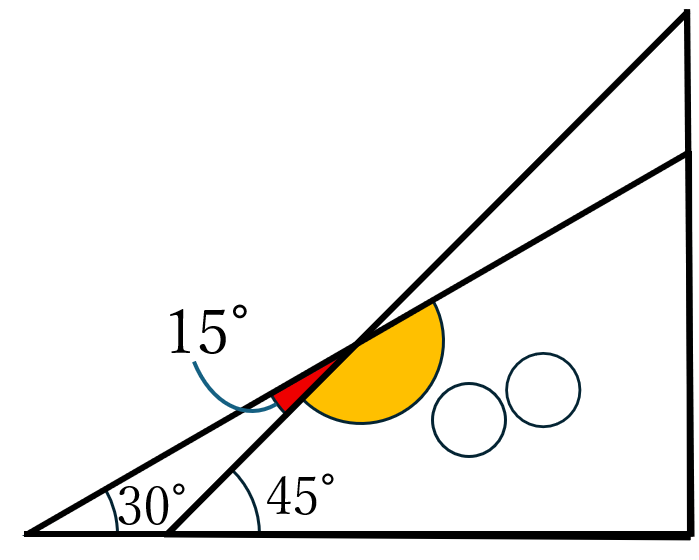
- または、180°から15°を引くという引き算の発想でも、165°を作ることが可能です。
このようにして、すべての15°刻みの角度(15°〜180°)を三角定規2枚で作れることがわかります。
◆授業展開のアイディア
【活動1】自由に角度を作って発表し合おう
- ねらい:角度の和・差の考え方に気づく
- 方法:2枚の三角定規を自由に使って様々な角度を作り、どのように作ったかを友達に説明する。
- 教師の工夫:できた角度を黒板に一覧でまとめ、そこから共通点(15°刻み)を見つけさせる。
【活動2】○○°をみんなで作ろう
- ねらい:協働的な学びと論理的思考の定着
- 方法:例えば「120°を作ってみよう」と目標角度を提示し、どのように作るかをグループで相談して挑戦。
- 教師の工夫:「どの角を組み合わせる?」「他の方法でも作れる?」といった多様な発想を促す声かけを。
◆おまけ:外角を使えば、もっと多くの角度が作れる!
これまで紹介してきたのは、三角定規の内角(定規の内側にできる角度)を使って作る角度でした。しかし、少し視点を変えて「外角」にも目を向けてみましょう。
◆外角ってなに?
三角定規を机に置いたとき、定規の外側にできる角度のことを「外角」と呼びます。たとえば、三角定規の30°の角の外側は、「180°−30°=150°」になります。
つまり、「ある角度の外側」=「180°−その角度」という考え方です。
◆外角を使って作れる角度の例
三角定規の角度は 30°、45°、60°、90° でした。これらの外角を求めてみると:
- 180° − 30° = 150°
- 180° − 45° = 135°
- 180° − 60° = 120°
- 180° − 90° = 90°
ここで、すでに出てきた角度と重なるものもありますが、これらを内角と組み合わせることで、さらに多くの角度を作ることができます。
◆外角と内角の組み合わせでできる角度の例
| 組み合わせ | 作れる角度 | 計算式の例 |
|---|---|---|
| 外角150° − 内角45° | 105° | 150° − 45° |
| 外角135° − 内角30° | 105° | 135° − 30° |
| 外角135° + 内角45° | 180° | 135° + 45° |
| 外角120° − 内角60° | 60° | 120° − 60° |
| 外角120° + 内角30° | 150° | 120° + 30° |
| 外角150° − 内角60° | 90° | 150° − 60° |
| 外角150° − 内角90° | 60° | 150° − 90° |
| 外角135° − 内角90° | 45° | 135° − 90° |
このように、外角を活用することで、「引き算」や「足し算」の発想が広がり、これまでにない角度の作り方に気づくことができます。
◆発展的な活動アイディア
- 「内角だけでは作れない角度を、外角を使って作ってみよう」
- 「何通りの方法で135°を作れるかな?外角も使ってみよう」
子どもたちにとって、「角度を作る方法は1つじゃない」という数学的多様性を実感できる貴重な学習になります。
また、180°以上の角度についても目を向けるとさらに視野が広がります。
例えば、下の図では300°を作っています。
そう考えると、さらに多くの角度を作ることができますね。
◆まとめ:三角定規は“探究”の宝庫!
三角定規を使った角度作りは、ただの作業で終わらせず、「気づき」や「発見」に満ちた授業にできます。特に外角を使う活動は、一歩踏み込んだ思考力・柔軟な発想力の育成につながります。
ちょっとした“おまけ”が、子どもたちの探究心を大きく刺激するかもしれません。ぜひ、子どもたちと一緒に、「角度っておもしろい!」という体験を共有してみてください。



コメント