※Word文書をプレビューで表示している場合、表記にズレが生じる可能性があります。
データをダウンロードした際には正しく表記されます。
5年生算数「合同な図形」の単元について、児童のノート見本を全時間分まとめました。
各ページの周囲には、授業づくりのポイントや発問例、児童がつまずきやすい箇所への支援方法なども掲載しています。これらのノートは、そのまま板書計画やワークシート作成の参考資料としてご活用いただけます。
使用教科書は東京書籍ですが、他社の教科書でも学習内容の大枠や流れは共通しているため、幅広い場面でご利用いただけます。
各画像はクリックするとPDF形式でダウンロード可能です。また、ページ下部には全ページ一括ダウンロード用リンクもご用意しています。
授業準備の効率化や板書の事前検討に、ぜひお役立てください。
第1時 ねらい:合同な図形とは何かを知る
活動の概要
三角形を切り取って、別の三角形の上に重ねてみる活動を通して、「ぴったり重なる図形」を合同な図形と捉える感覚を養います。
授業のポイント
- 「長さ」「広さ」「かさ」などと同様に、「合同な図形」もまずは直接比較から導入します。
- 裏返して重なる図形も合同であることに気づかせましょう。
- 身の回りにある「合同な形」に目を向けさせ、数学的視点で日常を捉える力を育てます。
例:身近な合同なもの
- 窓ガラス
- 両手のひら
- トランプのカード など
第2時 ねらい:対応する辺や角、頂点が等しいことを知る
活動の概要
合同な図形において「どの部分がどの部分と対応しているか」を学習します。
指導のポイント
- 四角形の名称のつけ方を確認します。
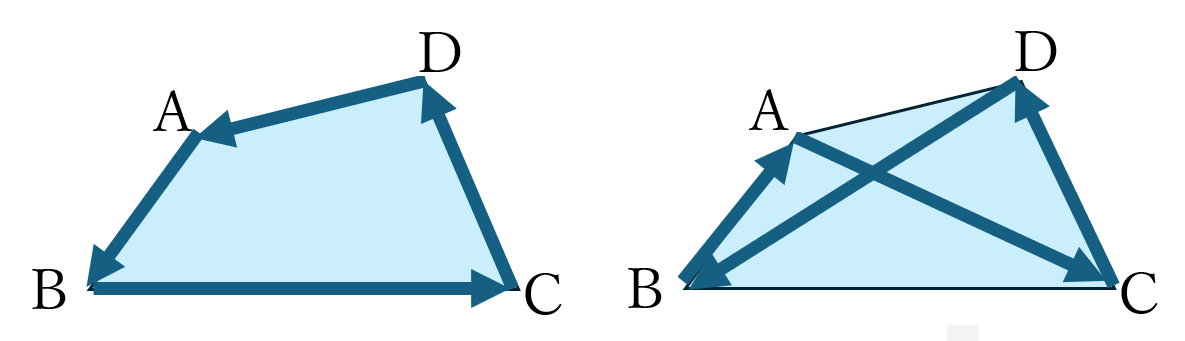
四角形ABCDや四角形CDAB,四角形DCBAのように、アルファベット通りに頂点を結んだ際、四角形が形作られるようにします。右のように四角形ACDBのような言い方は良くありません。 - 対応する辺や角を答える際には、「順序(向き)」も重要であることを指導します。
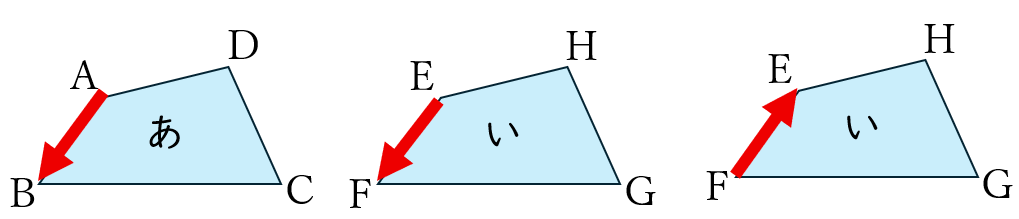
辺ABに対応する辺は、辺EFと答えるべきで、辺FEでは望ましくありません。テストの採点では誤答とまではしなくてもよいかもしれませんが、中学数学では誤答となる可能性が高いです。
発展的理解
- 前時では直接比較で合同性を調べましたが、本時では図形の構成要素を比較して判断します。
- 長さや広さなどと同様に、学習の流れは
→ 直接比較 → 直接比較できない場合の手法(間接比較・構成要素比較)
という流れを辿ります。
第3時 ねらい:四角形を構成する三角形が合同かを調べる
活動の概要
既習の四角形に対角線を引き、できた三角形同士が合同かどうかを調べます。
思考の流れ
- 本時では帰納的思考(実際に試して判断する)で合同かどうかを判断します。帰納的思考で判断するとは、「台形に1本の対角線を引いたら、できた三角形は合同ではなかった。他の台形も同じだろうから、台形に1本の対角線を引いてできた三角形は合同でない。」というように、1つの形で成り立つのだから、他の形でも成り立つであろうという考え方です。(帰納的思考法としては、1つの形だけで成り立つことを考えるのは、不十分ですが小学校算数では良しとしています。)
演繹的思考(参考)
- 指導上扱いませんが、三角形の合同条件を使って証明することも可能です。
例えば、「ひし形に1本の対角線を引いてできた2つの三角形を考える。ひし形は対頂角の大きさが等しいので、三角形の対頂角は等しい。また、ひし形は全ての辺の長さが等しいので、その対角線を作る2本の辺は等しくなる。よって、2つの三角形は2つの辺とその間の角が等しいため、合同となる。」これは、ひし形の性質を利用した証明なので、上記の帰納的思考法とは異なり、確実に正しいと言える精度の高いものです。 - 研究授業などで取り上げると、児童の論理的思考を深めるきっかけになります。
授業のまとめの例
- 各四角形ごとに「できた三角形は合同か?」を表で整理させ、「なぜ合同になるのか?」「なぜ合同にならないのか?」という特徴の違いに注目させてもいいです。数学的思考を深められます。
次につながる力
- 本時の四角形を対角線で三角形にわける考えは、今後の「多角形の内角の和」や「面積の求め方」の基礎になります。
第4時 ねらい:合同な三角形を作図する
活動の概要
与えられた情報から、合同な三角形をコンパスと定規で作図します。
指導の流れ
- 辺BCを先にかかせることで、作図のスタート地点を統一します。
- 頂点Aの位置を決めることが目的であると伝え、「どうすれば見つけられるか?」を考えさせます。
作図方法の共有パターン
- パターン①:各自自由な方法で作図 → うまくいったやり方を共有して条件を整理
- パターン②:教師が与えた条件で挑戦 → 成功例から条件を確認
(下のようなカードを切って提示し、児童にカードを選ばせてかいてもらいます。)
確認する3つの要素(合同な三角形をかく条件)
- 3辺の長さが等しい
- 2辺とその間の角が等しい
- 1辺とその両端の角が等しい
※小学校ではこれらを「合同条件」とは呼ばず、「合同な三角形をかくための要素」として扱います。
第5時 ねらい:合同な四角形をかく
活動の概要
前時の学習をもとに、2つの三角形を組み合わせて合同な四角形を作図します。
指導のポイント
- 四角形は三角形2つに分けて考えることで、既習の合同な三角形の知識が活用できることに気づかせます。
- 四角形の合同条件は扱いませんが、「知っていることを使って問題を解決する」経験を重視します。
第6時 ねらい:学習を振り返り、理解を定着させる
活動の概要
これまでの学習内容を振り返り、理解したことや苦手なことを整理します。
授業のポイント
- 「どんなことができるようになったか」「どこでつまずいたか」に着目させ、自己評価とメタ認知を促します。
- 単元全体の学習の流れを再確認し、他の単元とのつながりを意識させると、より深い理解につながります。
最後に
この「合同な図形」単元は、図形感覚だけでなく、論理的に筋道を立てて考える力を育てる内容です。
各時のノート例や発問例を活用いただくことで、児童の思考を促す効果的な授業づくりにつながります。
PDF資料とともに、現場の授業改善や教材研究の一助となれば幸いです。


コメント