※Word文書をプレビューで表示している場合、表記にズレが生じる可能性があります。
データをダウンロードした際には正しく表記されます。
「比」の学習は、これまでの算数学習の集大成ともいえる単元です。
ここには「割合」や「比例」、「約分」など、これまでに学んだ考え方が複合的に関わっています。
そのため、児童の既習知識とのつながりを意識して授業を展開することが大切です。単元全体の流れとともに、指導のポイントや誤答例を交えて紹介します。また、授業を行った際に実際に使ったノート計画も貼りますので、参考になれば幸いです。
第1時:比とは何かを知ろう
内容
- 「比」とは、2つの数量の関係をa:b(a対b)で表すことを学びます。
- ウスターソースとケチャップで作るハンバーグソースを題材に、量が増えても比(味)が変わらないことに気づかせます。
- 身近にある「○対□」の場面を見つけることも理解を深めるために有用です。
身近にある「○対□」の例
- めんつゆの希釈(水:めんつゆ=1:3)
- スポーツの得点(42対51)
- 髪型(七三分け)
- 地図の縮尺(1:10,000)
- 写真の縦横比(4:3)
指導のポイント
- 「1とみる」「全体を1とする」割合の考えに苦手意識のある児童が多いため、図や具体物で可視化できるといいです。
- 「比=割合の一種」であることにふれ、「比は割合よりも幅広い表し方ができる」と伝えるのも効果的です。
第2時:比と割合の関係に気づこう
内容
- 2:3という比について、どちらをもとにするかによって表現が変わることを学びます。
- 一方をもとにした量について、割合と同様に「比べられる量÷もとにする量」で求められることをおさえます。
指導のポイント
- 小5でつまずきやすい「もとにする量」「比べられる量」が、どの数値のことを指しているのか、見極めに注意です。
- ウスターソース2、ケチャップ3なら「ケチャップを1と見たとき、ウスターソースは2/3」という意味であることを確認します。(小5の割合と同じ考えです。)
- 「2:3 = 2÷3」ではなく、「2:3 → 2÷3」と表記するように伝えます。
よくある誤答例
- 「比の順番」を逆にする(例:3:2とする)
- 分数表記のとき、分母・分子の順を混同する(例:3/2にする)
第3時:比の性質を知ろう
内容
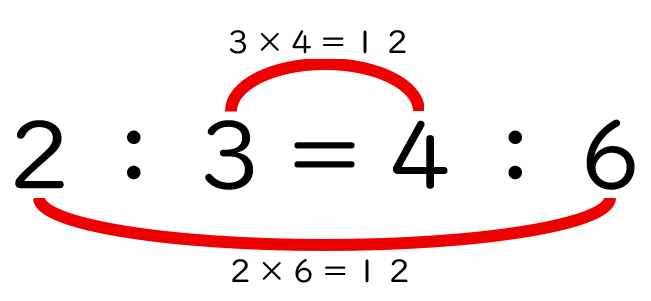
- 2:3 = 4:6のように、両方に同じ数をかけても比の関係は変わらないことに気づく学習です。
指導のポイント
- 「比はわり算と同じ性質を持っている」ということに気づかせます。
- 2:3という比ですが、これを2÷3という式で考えれば、割る数と割られる数に同じ数をかけても変わらないというわり算の性質と何も変わりません。
ちなみに、2:3をわり算の式として表記する国もあります。
- 教科書に載っている比の性質以外にも、触れると理解が深まります。
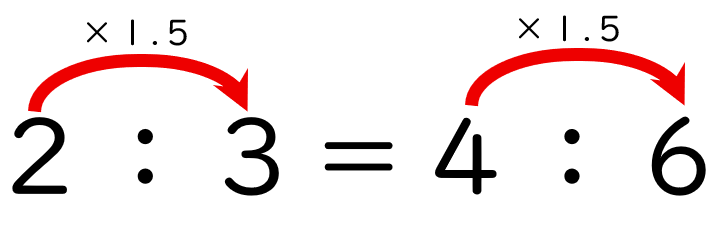
第4時:比を簡単にしよう
内容
- 比をできるだけ小さい整数の比にする学習です。(例:12:8 → 3:2)
指導のポイント
- 「約分」とのつながりを意識させたいです。
- 公約数や公倍数といった言葉の復習も行いたいです。
- 分数との類似性にもふれると理解が促進されます。
第5時:小数・分数の比を整数にしよう
内容
- 小数・分数で表された比を最も小さい整数の比に変える方法を考えます。
指導のポイント
- 小数なら10倍・100倍、分数なら通分や分母の公倍数をかけて整数にすれば、比を簡単にできます。
- 比較的、既習事項を活用して解きやすい問題なので、児童同士で解法を共有させやすい学習です。
第6時:比から一方の量を求めよう
内容
- 比と一方の量から、もう一方の量を求める学習です。
指導のポイント
- 線分図を活用して数量関係を可視化します。一人で図が書けるようにしたいです。
- 「1にあたる部分はいくつか?」→「全体は?」の流れで思考させます。
第7時:全体の量から一部の量を求めよう
内容
- 全体と比から、部分の量を求める学習です。
指導のポイント
- 式に頼るのではなく、図を使って関係を整理するよう指導します。
- 問題文では「3:5」という比が書かれていますが、解法では「3:5」の比は使いません。「何がわかっていて、何を求めるのか」を図をもとに確認する必要があります。
第8時:学習のまとめ
内容
- 練習問題を通じて、学習内容の理解を深めます。
- できるようになったことや、まだ苦手な学習内容に気づかせ、自己評価とふり返りを行います。
おわりに:比と割合の本質的な違いとは?
| 観点 | 比 | 割合 |
|---|---|---|
| 意味 | 2つの数量の対等な関係性 | ある数量が他の数量に対してどれくらいか |
| 表現方法 | a:b | a÷b、小数、百分率 |
| 「もと」 | 特定されないことが多い | 必ず「もとにする量」がある |
児童にとって、「割合と比の違い」は混乱のもとになりやすいですが、
「割合はもとにする量がはっきりしているが、比は量同士の関係を対等に見る」
という視点を押さえると、より深い理解につながります。


コメント