※Word文書をプレビューで表示している場合、表記にズレが生じる可能性があります。
データをダウンロードした際には正しく表記されます。
はじめに
わり算には「包含除(ほうがんじょ)」と「等分除(とうぶんじょ)」の2つの意味があります。
「名前は聞いたことがあるけど、どう違うのかよくわからない…」
そんな先生方も少なくないかもしれません。
包含除と等分除の違いや見分け方を、小学校の算数指導の視点から、図や例を交えて、どこよりも丁寧に解説します。
まずは問題から考えてみましょう
問題:
いちごが15こあります。このいちごを1人に3こずつ分けると、何人に分けられますか?
式に表すと 15 ÷ 3 ですね。
この問題は、包含除の考え方になります。
◆ 包含除とは?
包含除とは、「〇こずつで、いくつ分とれるか?」を問う場面です。
上の例で言えば、「3こずつで、何人に分けられるか?」という問いです。
図にすると、いちごを「3こずつ丸で囲んでいく」イメージになります。

🔹 式: 15(個) ÷ 3(個)
🔹 意味: 「3こ分(=1人分)は何回取れるか?」
🔹 助数詞: 割られる数と割る数の単位(助数詞)は同じになります。
◆ 等分除とは?
等分除とは、「〇人で等しく分けたら、1人分はいくつになるか?」を問う場面です。
同じいちご15こを、3人で平等に分けたとき、1人分は何こか?というのが等分除です。
図にすると、1人に1個ずつ配るイメージになります。
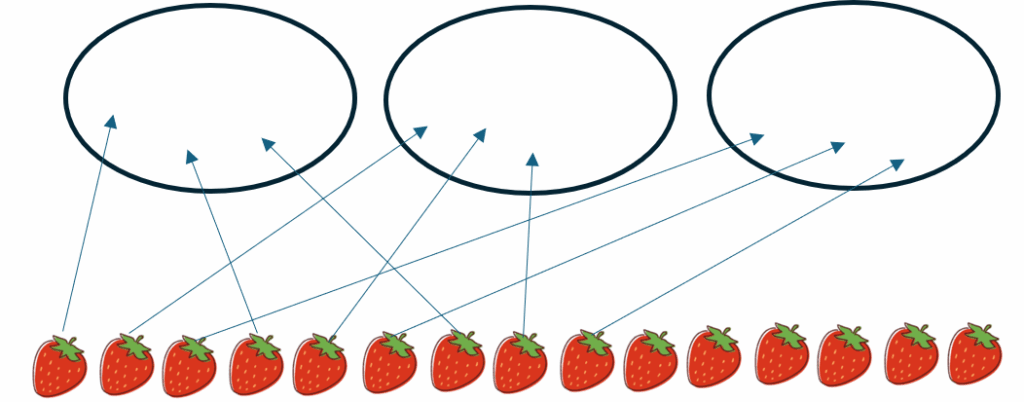
🔹 式: 15(個) ÷ 3(人)
🔹 意味: 「3人で分けたら、1人分は何こか?」
🔹 助数詞: 割られる数と割る数の単位(助数詞)は異なります。
かけ算の意味から、わり算をとらえる
小学2年生では、かけ算の意味を次のように学びます:
(1つ分の大きさ) ×(いくつ分)=(全体の大きさ)
この関係をもとに、わり算の意味を分類すると…
| 区分 | 式 | 求めるもの | わかりやすい表現 |
|---|---|---|---|
| 等分除 | (全体の量)÷(いくつ分) | 1つあたりの量 | 「3人で分けると1人分は?」 |
| 包含除 | (全体の量)÷(1つあたりの量) | いくつ分あるか | 「3個ずつだと何人分?」 |
同じわり算 a ÷ b を、□を使ってかけ算の形で表したとき、
- 等分除:□×b=a →(例)□ × 3人 = 15個(□が「1人分の大きさ」)
- 包含除:b×□=a →(例) 3個 × □ = 15個(□が「いくつ分」)
と、どちらもかけ式は同じでも「問われているもの」が違うために、わり算の式が異なるのです。
教科書ではどのように扱われているか
- 小学3年生の教科書では、等分除から先に学習します。
理由は、「分ける」という行為が生活の中でも身近で、具体的にイメージしやすいからです。 - 一方、小数や分数のわり算では、包含除から学習することが多いです。
なぜなら、具体的にいくつ分とれるかを操作的に考えやすいからです。
小数・分数のわり算と包含除・等分除
たとえば、
3/5 ÷ 1/2 の意味を考えてみましょう。
- 「3/5を1/2で割る」と言ったとき、「3/5の中に1/2はいくつあるか?」というのは包含除の考えです。
- また、「3/5を1/2ずつに分けると何人分か?」と考えるのも包含除です。
一方、等分除の視点で分数のわり算を見ると、
「1/2に対する値が3/5にとき、1に対する値は何か?」と考えることとなります。
(別の言い方をすると「3/5は1/2を1としたときのいくつ分か。」)
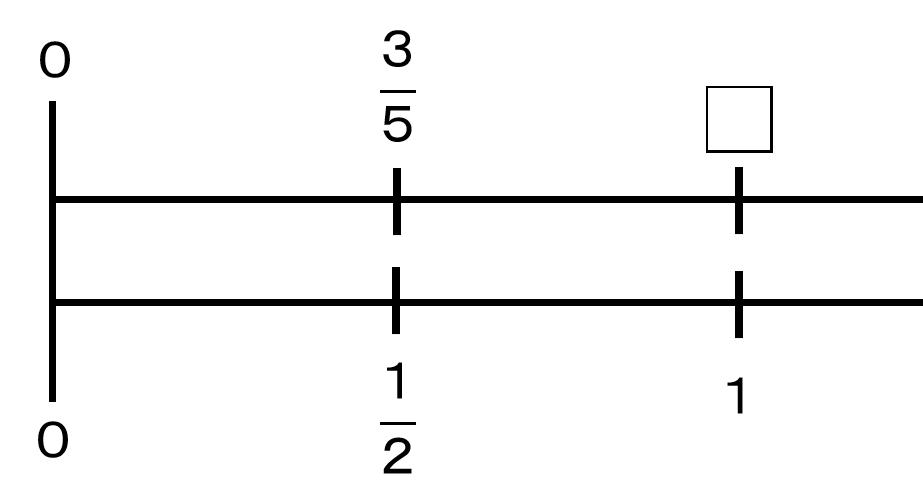
つまり、分数のわり算では、包含除・等分除の区別がより意識されるようになります。
筆算で登場する「等分除」
たとえば、
90 ÷ 3 の筆算を学ぶとき、3こずつ90個を丸で囲んで…という包含除的なアプローチは現実的ではありません。

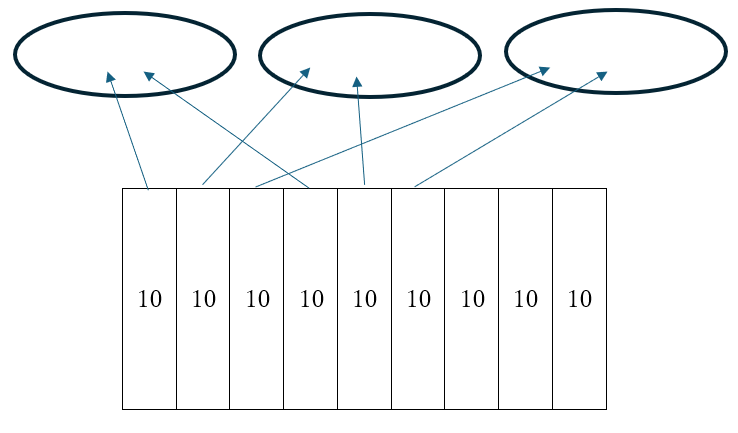
教科書では、「90を3人で等しく分けると?」という等分除の状況で導入されます。
たとえば「90は、10が9こある」と考えて、それを3人で分けるというのは、等分除です。
割合を求めるときのわり算
時速や割合の計算も、わり算の意味理解と関係します。
- 例)時速=道のり ÷ 時間
→「1時間あたりどれだけ進んだか?」= 等分除の考え - 例)割合=比べる量 ÷ 基準量
→「1あたりに直す」= 等分除の考え
このように、割合を求める場面のわり算は、ほとんどが等分除の考え方です。
まとめ:見分け方のポイントと教材研究へのヒント
| 項目 | 等分除 | 包含除 |
|---|---|---|
| 求めるもの | 1つ分の大きさ(単位量) | いくつ分とれるか(回数・個数) |
| 助数詞 | 異なる(例:個 ÷ 人) | 同じ(例:個 ÷ 個) |
| 式の意味 | □ × 割る数 = 全体 | 割る数 × □ = 全体 |
| イメージ | 配る、等しく分ける | 同じ大きさで何回とれるか |
| 理解のしやすさ | 意味理解に有効 | 計算方法の習得に有効 |
🔎 教科書や問題文を見るときに、「これは包含除かな?等分除かな?」と問いを立てることが、わり算の教材研究の第一歩です。
おわりに
等分除と包含除を意識して授業づくりを進めていくと、子どもたちの理解がより深く、意味と手続きのつながりが見えてきます。
「このわり算はどちらの意味だろう?」と問い直しながら教材を見ることで、子どもがつまずくポイントにも気づきやすくなります。




コメント