※Word文書をプレビューで表示している場合、表記にズレが生じる可能性があります。
データをダウンロードした際には正しく表記されます。
小学5年生では、「異分母分数のたし算」の学習が始まります。この学習では、分母が異なる分数を通分し、計算する力が求められます。
たとえば、次のような計算です。
3/4 + 2/5
⇒ 15/20 + 8/20
⇒ 23/20
しかし、児童の中には次のような誤答をしてしまうことがあります。
3/4 + 2/5 = 5/9
これは、「分子+分子、分母+分母」と分子同士、分母同士でたし算をしてしまう典型的な誤りです。多くの児童が一度はこのようなミスを経験しますし、大人でもつい納得しそうになります。
では、この「3/4+2/5=5/9」は、本当に間違いなのでしょうか?
間違っているのに、なぜか納得してしまう理由
次のような具体場面を使って、誤答がどうして生まれたのかを探ってみましょう。
■ 場面設定:2つのグループ
Aグループには、4人の子どもがいます。そのうち3人が男の子です。

→ 男子は 3/4
Bグループには、5人の子どもがいます。そのうち2人が男の子です。

→ 男子は 2/5
では、AグループとBグループを合体させて、全体の中で男の子の割合を考えてみましょう。
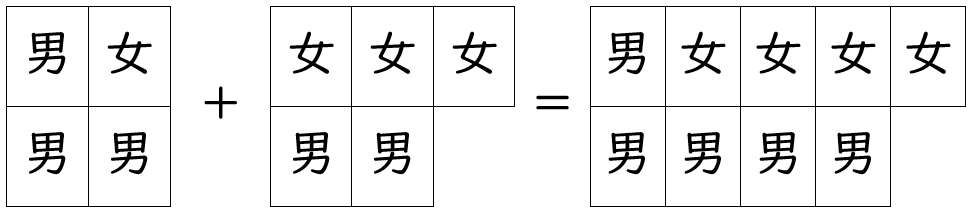
合体後の全体:
- 人数:4人+5人=9人
- 男子の人数:3人+2人=5人
→ 男子の割合は 5/9
この結果を見ると、「3/4+2/5=5/9」という式が“正しいように見える”のです。実際、割合としては合っています。しかしこれは、単純なたし算とは違う概念を表しています。
本当の問題点は「分数の意味」にある!
ここで大切になるのが、「分数の意味」です。実は、分数には大きく分けて2つのタイプがあります。
◆ ① 分割分数(分数=全体を等しく分けたうちのいくつ分)
これは教科書で最も基本的に扱われる分数の意味です。
例)3/4
→ 1つのホール(ピザ、ケーキ、1m など)を4等分して、その3つ分を取るという考え方です。
たし算をするときも、「同じものを基準にして」数を合わせます。たとえば、1つのケーキの3/4と、もう1つのケーキの2/5を合わせるときは、両方のケーキを同じサイズ(同じ単位)に変えてから計算する必要があります(=通分)。
◆ ② 量分数(割合・比としての分数)
こちらは、「全体に対してどれだけの割合か」を示すときに使われます。
例)Aグループの3/4が男の子というのは、「Aグループ全体の人数」が基準です。
同様に、Bグループの2/5が男の子というのも、「Bグループ全体の人数」が基準です。
つまり、基準がちがうのです。
このとき、「3/4+2/5=5/9」は、割合の合成(全体が別々のグループ)で求めた新たな割合です。これは「割合の平均」に近い考え方で、たし算のルールとしては正しくありません。
まとめ:なぜ「3/4+2/5=5/9」は間違いなのか?
- 「3/4」「2/5」の基準となる全体が違う(4人、5人)。
- 分数のたし算は、共通の基準にそろえる(通分)必要がある。
- 「割合の合成」と「分数のたし算」は、目的も意味も異なる。
授業で活用するためのポイント
- 「分数の意味には2種類ある」ことを、児童にわかりやすく紹介する。
- 誤答「3/4+2/5=5/9」が、割合を合成した結果であることを説明する。
- 通分が必要になる「分割分数」との違いを、具体場面(人数、図など)で比較させる。
- 実際のたし算は「3/4+2/5=23/20」であることを、共通の基準(通分)によって導けるようにする。
おわりに
児童が「3/4+2/5=5/9」と答えてしまうのは、間違いではあるけれど、思考の根っこにある感覚は大切にしたい誤りです。この誤りをきっかけにして、分数の意味や使い方の違いを丁寧に学習することができます。
ぜひ、導入場面でこの問いを使ってみてください。児童たちの「なんで!?」という反応から、学びが深まるはずです。



コメント